Уравнение мгновенного тока индуктивной катушки

Где применяется катушка индуктивности

Свойства индуктивной катушки своеобразные, небольшая доработка добавляет ей новые свойства, что делает ее весьма востребованной. Рассмотрим лишь некоторые области, где она с успехом нашла свое применение:

1. Конечно, это сама электротехника. Сочетания катушки с резистором или конденсатором делает ее способной задерживать или пропускать определенные частоты.
2. В импульсной технике катушка индуктивности выступает в качестве накопителя энергии.
3. Соединенные определенным образом катушки образуют различные по назначению трансформаторы.
4. Катушка индуктивности дает возможность повышать напряжение постоянного тока.
5. Электромагнит – еще одно применение катушки.
6. Используются для выплавки металла в доменных печах.
7. Особенно в старых приемниках катушка часто выступала в качестве антенны.
8. Современные индукционные плиты никак не могут работать без катушки индуктивности.
9. Если сердечник катушки соединить с подвижным механизмом – получится отличный датчик движения.
10. Индукционные магнитометры имеют основным элементом катушку индуктивности.
11. Для ускорения частиц в лабораториях также применяют своеобразную катушку.
12. Специальные накопителя энергии не могут обойтись без этого элемента.

Это лишь основные области применения, но уже по этому списку видно, что катушка – хороший труженик. Рассмотрим некоторые области применения более подробно.

Катушка как электромагнит

Для получения электромагнита используют сердечник из магнитомягкого материала. Для этого подходят:

металлы: сталь, чугун;
сплавы железа с никелем или кобальтом.

Интересно. Если магнитопровод сделать цельным, тогда у него будут большие потери, поэтому его собирают из отдельных листов.

Электромагниты могут работать как от постоянного, так и переменного тока. Причем электромагнит постоянного тока может быть нейтральным, когда притягивающая сила образуется независимо от направления движения тока, и поляризованным. В этом случае используется две обмотки: основная и поляризующая. Основная создает магнитный поток, а вторая направляет его в нужном направлении.

Электромагниты, работающие на переменном токе, вырабатывают переменное магнитное поле, но на сердечник оно действует в одном направлении. Однако сила притяжения меняется от нуля до максимума. Частота притяжения вдвое выше частоты тока.

Катушка как источник ЭДС

Эта особенность используется в индукционных плитах. Катушка, расположенная прямо под плитой, при работе создает вокруг себя электромагнитные волны. Эти волны, воздействуя на материал кухонной посуды, нагревают ее. Причем сама плита остается достаточно холодной, нагревается лишь от самой посуды. Такие плиты перестают работать, если посуды на ней нет, что делает их безопасными в пожарном отношении.

Более мощные устройства используются на сталелитейных заводах. Доменную печь делают круглой и обвивают ее толстыми, обычно медными проводами. Когда по проводу пропускают ток большой мощности и частоты, создается мощное электромагнитное поле, воздействующее на металл, находящийся в печи. От действия этого поля металл нагревается и плавится.

Это же устройство, но меньшего размера используется, когда необходимо нагреть небольшой кусок металла, например, для ковки.

Катушки индуктивности в качестве трансформатора

В первых двух вариантах обычно используется одна катушка, но если соединить две и более катушки и по одной из них пропустить ток, то получится интересный момент. В этой катушке появится наведенная ЭДС. Она окутает все находящиеся в ее поле другие катушки и в них появится ток. Но это еще не все.

Регулируя число витков в других катушках, можно подобрать необходимое напряжение. То есть, число витков может увеличивать или уменьшать напряжение относительно напряжения, проходящего по рабочей катушке. Чтобы такая передача была более продуктивной, используют один из видов сердечника:

стержневой;
броневой;
тороидальный.

Конструкция сердечника особого влияния на трансформатор не оказывает, это больше предпочтение производителя. Осталось рассмотреть еще одну удивительную особенность катушки индуктивности – способность генерации.

Мощность реальной катушки

Мгновенная мощность катушки

p = ui = Umsin(ωt+φ) * Imsinωt

Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты. При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).

Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).

Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.

Согласно выводам полученных в этих предыдущих (первая, вторая) статьях — в активном сопротивлении P = URI Q = 0; а в индуктивном Р = 0; Q = ULI.

Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении XL. Подставляя значения UR = Ucosφ и UL = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:

P = UIcosφ (13.19)

Q = UIsinφ (13.20)

Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;

S = UI = I2Z (13.21)

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

(13.22)

Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить

cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)

Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).

Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности P/S = = cosφ называют коэффициентом мощности.

Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.

Терминология

Стандартизированные термины:

Индуктивная катушка

— элемент электрической цепи, предназначенный для использования его индуктивности (ГОСТ 19880-74, см. термин 106).

Катушка индуктивности

— индуктивная катушка, являющаяся элементом колебательного контура и предназначенная для использования её добротности (ГОСТ 20718-75, см. термин 1).

Электрический реактор

— индуктивная катушка, предназначенная для использования её в силовой электрической цепи (ГОСТ 18624-73, см. термин 1). Одним из видов реактора является токоограничивающий реактор, например, для ограничения тока короткого замыкания ЛЭП.

При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника часто называют дросселем

, а иногда реактором. Стоит отметить, что такое толкование нестандартизированного термина«дроссель» (являющегося калькой с нем.Drossel) пересекается со стандартизированными терминами. В случае если работа данного элемента цепи основана на добротности катушки, то такой элемент следует называть «катушкой индуктивности», в противном случае «индуктивной катушкой».

Цилиндрическую катушку индуктивности, длина которой намного превышает диаметр, называют соленоидом

, магнитное поле внутри длинного соленоида однородно. Кроме того, зачастуюсоленоидом называют устройство, выполняющее механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, илиэлектромагнитом . В электромагнитных реле называютобмоткой реле , реже — электромагнитом.

Нагревательный индуктор

— специальная катушка индуктивности, рабочий орган установок индукционного нагрева.

При использовании для накопления энергии (например, в схеме импульсного стабилизатора напряжения) называют индукционным накопителем

или накопительным дросселем.

Влияние числа витков и способа намотки

Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:

большим количеством витков на единицу длины;
укрупнением поперечного сечения;
установкой в центральной части сердечника с ферромагнитными характеристиками.

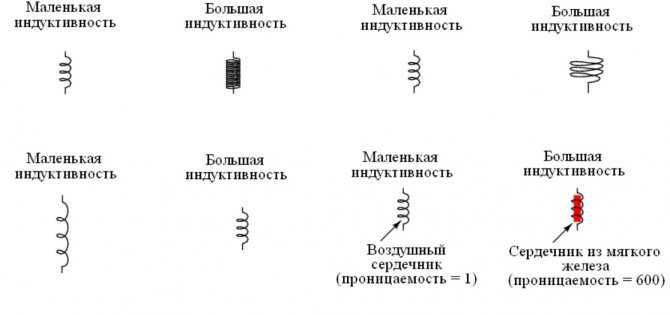
От чего зависит индуктивность катушки, примеры типовых решений

Индуктивность одновиткового контура и индуктивность катушки

Для расчета элементарной конструкции подойдет преобразованная первая формула:

Ф = L * I.

Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:

Ψ = n * Ф.

Аналогичным образом:

Ln = L1 * n.

В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.

Советуем изучить Mimo антенна 4g lte своими руками

Индуктивность соленоида

Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.

Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:

количества витков (N);
тока (i);
плотности намотки (n – число контуров на единицу длины);
площади поперечного сечения (S);
объема (V = S * l).

Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):

В = m0 * N * (i/l) = m0 * n * I;
Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
L = m0 * N2 * (S/l) = m0 * n2 * V.

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:

L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),

где:

2π * rL – длина рабочего элемента со средним радиусом rL;
R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.

Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I 2

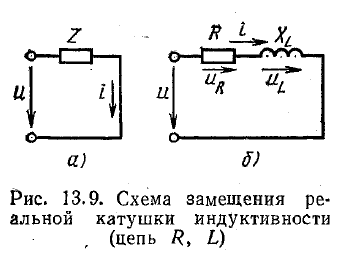
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = I_msinωt. Требуется определить напряжение в цепи и мощность. При переменном токе в катушке возникает э. д. с. самоиндукции e_Lпоэтому ток зависит от действия приложенного напряжения и эдс e_L. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

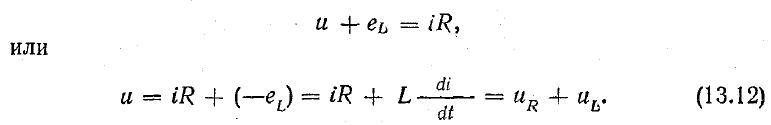
Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых u_R равно падению напряжения в активном сопротивлении, а другое u_L уравновешивает эдс самоиндукции.

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б). Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — u_R совпадает по фазе с током, U_Lопережает ток на 90°.

u = R*I_msinωt + ωLI_msin(ωt+π/2).

Последовательное и параллельное соединение индуктивностей

Индукторы могут быть соединены последовательно или параллельно, что обеспечивает ряд новых функций.

Параллельное соединение

Если индукторы соединены параллельно, напряжения всех компонентов равны, а ток (переменный) распределяется обратно пропорционально индуктивности компонентов.

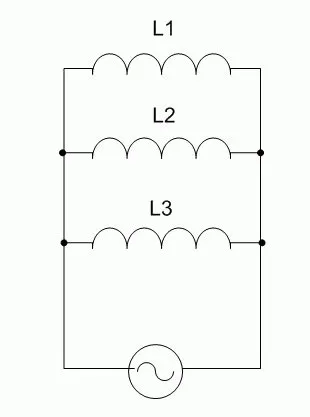
Общая индуктивность цепи определяется как 1/L = 1/L₁+ 1 / L₂+ 1 / L₃. Эта формула действительна для любого количества элементов и упрощается до вида L = L для двух катушек.₁* L₂/ (L)₁+ L₂). Очевидно, что результирующая индукция меньше, чем у элемента с наименьшим значением.

Последовательное соединение

В этом типе соединения один и тот же ток протекает через цепь, состоящую из катушек, а напряжение (переменное!) каждого компонента цепи распределяется в соответствии с индуктивностью каждого компонента.

Общая индуктивность равна сумме всех индуктивностей и больше, чем индуктивность элемента с наибольшим значением. Поэтому это соединение используется, когда необходимо увеличить индукцию.

Схема замещения реальной катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной B_L проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее. Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: I_G —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; I_L — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие I_G и I_L образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается I_а. Для катушки по схеме на рис. 13.12, б I_a = I_G.

Составляющая тока в реактивном элементе

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки I_р = I_L .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = I_G/U и индуктивная В_L = I_L/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

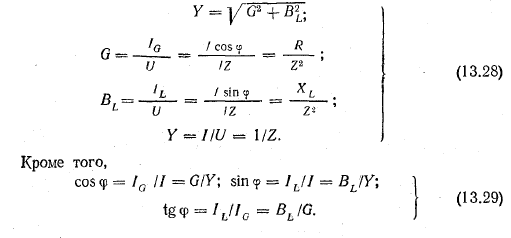
Комплексные числа. Основные законы электрических цепей в комплексной форме

Определение 1 Комплексное число – это число вида а + сi, где а и с — вещественные числа, а i — мнимая единица, то есть число для которого выполняется равенство i(2) = -1.

Множество комплексных чисел может обозначаться С. Вещественные числа рассматриваются как частный случай комплексных чисел и имеют следующий вид а + 0i. Главное свойство комплексного числа заключается в том, что в нем выполняется основная теорема алгебры, то есть многочлен n-ой степени (n ⩾ 1) имеет n корней. Также доказано, что система комплексных чисел логически непротиворечива.

Замечание 1

Основная теорема алгебры представляет собой утверждение, что поле комплексных чисел алгебраически замкнуто, то есть любой многочлен, который отличен от константы, с комплексными коэффициентами имеет минимум один корень в поле комплексных чисел. Такое утверждение справедливо для многочленов с вещественными коэффициентами, потому что всякое вещественное число является комплексным с нулевой мнимой частью.

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

Необходимость применения комплексных чисел появилась в результате решения кубических уравнений, так как в формуле Кардано под квадратным корнем получалось отрицательное число. В изучение комплексных чисел большой вклад внесли такие ученые, как Эйлер, Гаусс и Декарт. Свойства комплексных чисел позволяют использовать их в решении разнообразных задач в области теории упругости, математики, обработке сигналов, теории колебаний, электромагнетизме, теории управления и т.п.

Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как цепи постоянного электрического тока, с заменой постоянных величин следующим образом:

Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Курсовая работа Комплексные сопротивления и проводимости 470 ₽ Реферат Комплексные сопротивления и проводимости 260 ₽ Контрольная работа Комплексные сопротивления и проводимости 240 ₽

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

К основным законам электроцепей относятся:

Закон Ома.
Первый закон Кирхгофа.
Второй закон Кирхгофа.

В комплексной форме закон Ома будет иметь следующий вид:

Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ

Первый закон Кирхгофа в применении к узлу в комплексной форме выглядит следующим образом:

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

Второй закон Кирхгофа, применительно к контуру цепи, в комплексной форме можно записать следующим образом:

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Достоинство выражения законов электрических цепей в комплексной форме заключается в том, что в них учитываются связь между действующими значениями напряжения и тока, а также сдвиг фаз между ними.

Закон Фарадея

Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.

Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.

Формула закона электромагнитной индукции Фарадея выглядит следующим образом:

Рис. 2. Формула закона электромагнитной индукции

И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.

Основные понятия и законы электростатики

Закон Кулона:сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:

Коэффициент пропорциональности в этом законе

В СИ коэффициент k записывается в виде

Потенциалом электрического поля называют отношение потенциальной энергии заряда в поле к этому заряду:

Проекция напряжённости электрического поля на какую-нибудь ось и потенциал связаны соотношением

Электроёмкостью тела называют величину отношения

Основные понятия и законы постоянного тока

Электрический ток — направленное движение электрических зарядов. В разных веществах носителями заряда выступают элементарные частицы разного знака. За положительное направление тока принято направление движения положительных зарядов. Количественно электрический ток характеризуют его силой. Это заряд, прошедший за единицу времени через поперечное сечение проводника:

Закон Ома для участка цепи имеет вид:

При параллельном соединении величина, обратная сопротивлению, равна сумме обратных сопротивлений:

где t — время, I — сила тока, U — разность потенциалов, q — прошедший заряд.Закон Джоуля-Ленца:

Основные понятия и законы магнитостатики

Характеристикой магнитного поля является магнитная индукция ➛B. Поскольку это вектор, то следует определить и направление этого вектора, и его модуль. Направление вектора магнитной индукции связано с ориентирующим действием магнитного поля на магнитную стрелку. За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле. Направление вектора магнитной индукции прямолинейного проводника с токам можно определить с помощью правила буравчика:если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения рукоятки буравчика совпадает с направлением вектора магнитной индукции. Модулем вектора магнитной индукции назовём отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током , к произведению силы тока на длину этого участка:

Основные понятия и законы электромагнитной индукции

Если замкнутый проводящий контур пронизывается меняющимся магнитным потоком, то в этом контуре возникает ЭДС и электрический ток. Эту ЭДС называют ЭДС электромагнитной индукции, а ток — индукционным. Явление их возникновения называют электромагнитной индукцией. ЭДС индукции можно подсчитать по основному закону электромагнитной индукции или по закону Фарадея:

Электромагнитные колебания и волны

Колебательным контуром называется электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью C и катушки с индуктивностью L (см. рис. 7).

Для свободных незатухающих колебаний в контуре циклическая частота определяется формулой

Период свободных колебаний в контуре определяется формулой Томсона:

Ток, текущий через катушку индуктивности, по фазе отстаёт от напряжения на π/2 или на четверть периода. Напряжение опережает ток на такой же фазовый угол.

Трансформатором называется устройство, предназначенное для преобразования переменных токов. Трансформатор состоит из замкнутого стального сердечника, на который надеты две катушки. Катушка, которая подключается к источнику переменного напряжения, называется первичной обмоткой, а катушка, которая подключается к потребителю, называется вторичной обмоткой. Отношение напряжения на первичной обмотке и вторичной обмотке трансформатора равно отношению числа витков в этих обмотках:

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

Длина обмотки превышает диаметр в несколько раз;
Толщина обмотки меньше диаметра катушки также в несколько раз.

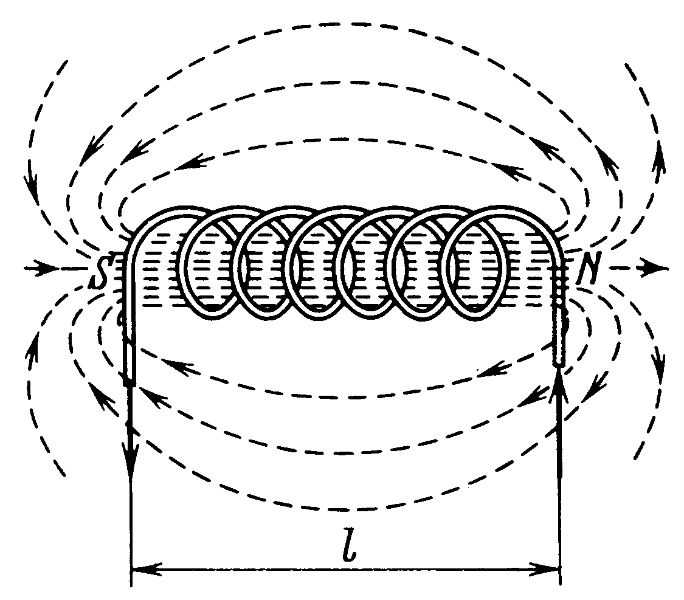
Соленоидальный тип катушки

Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

µ0 – магнитная постоянная;
N – количество витков;
S – площадь поперечного сечения обмотки;
l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Общее описание

Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.

Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).

Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.

Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.

Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.

Катушка индуктивности в цепи постоянного тока.

И, в первую очередь, разберемся, что происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? Однозначно нет. Ведь постоянный ток можно «включать/выключать», и как раз в моменты переключения и происходят все ключевые процессы. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?

Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:

\varepsilon_s = -\frac{d\Phi}{dt}

Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна.

А далее произойдет следующее — поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот, будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:

На первом графике мы видим входное напряжение цепи — изначально цепь разомкнута, но при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.

Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый).

Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:

После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции, в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).

Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является как раз индуктивность катушки:

\varepsilon_s = -L\medspace\frac{dI}{dt}

На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.

Важный (!) нюанс заключается в том, что напряжение на катушке при описанных переходных процессах может достигнуть весьма значительных величин. Это, в свою очередь, легко может привести к выходу из строя тех или иных компонентов, входящих в состав цепи. Например, при управлении индуктивной нагрузкой при помощи ключа на транзисторе явление возникновения ЭДС самоиндукции с впечатляющей вероятностью приведет к выходу транзистора из строя. Для защиты от этого параллельно индуктивной нагрузке ставят защитный диод, но сегодня речь не об этом, поэтому для данного аспекта я опубликую отдельный материал с рассмотрением основных нюансов.

Реактивное сопротивление катушки индуктивности

С помощью нехитрых умозаключений, физиками была выведена формула:

где

Х_L — реактивное сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность, Гн

В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.

Видео про катушку индуктивности:

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

L=Ф/I.

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

L=L1∙N2.

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.